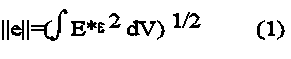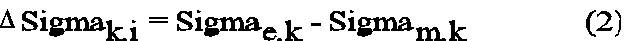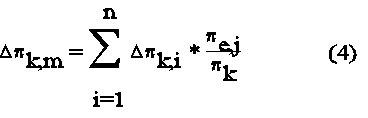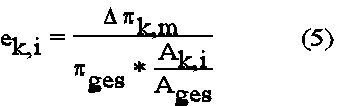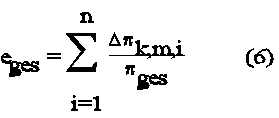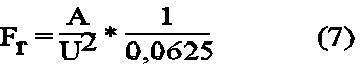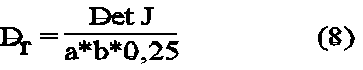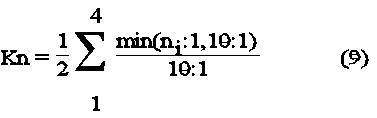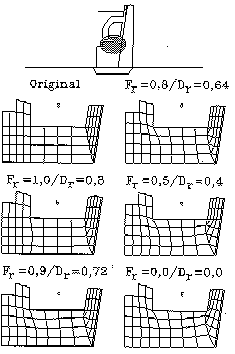Automatische Generierung von FE-Netzen für Scheibenkonstruktionen am Beispiel von Gewichtsstaumauern
Automatic generation of FE meshes for slab constructions by example of gravity dams
Kurzform der Dr.-Arbeit von M. Hoffmann
Die Abbildungen erscheinen hier in Miniform. Um eine Abbildung größer zu sehen, klicken Sie darauf !
Der Bericht behandelt Finite-Elemente-Berechnungen von Scheibenkonstruktionen, z.B. für Gewichtsstaumauern. Es wird ein Algorithmus für die Netzerzeugung gezeigt. Zunächst wird ein Fehlerindikator vorgestellt, dann der Aufbau von FE-Netzen erläutert und anschließend wird eine Methode gezeigt, mit der man optimale FE-Netze erzeugen kann. Als Anwendungsbeispiel dient die Generierung des FE-Netzes für eine Gewichtsstaumauer.
Inhaltsverzeichnis
1. Zielsetzung
2. Genauigkeit einer FE-Berechnung
3. Fehlerindikator für Elastizitätsprobleme
3.1 Vergleich mit exakter Lösung
3.2 Fehlerindikator aus Spannungssprüngen
4. Aufbau von FE-Netzen
4.1 Elementeigenschaften
4.1.1 Elementart
4.1.2 Seitenverhältnis
4.1.3 Elementform
4.2 Netzformen
4.2.1 Unregelmäßigkeit
4.2.2 Unsymmetrie und Größenverhältnis
5. Generierung optimaler FE-Netze
5.1 Netzglättung
5.2 Adaptive Netzverfeinerung
5.2.1 h- und p-Version
5.2.2 Steuerungsparameter
5.2.3 Fuzzysteuerung
6. Fallbeispiel: Staumauer mit Dreieckprofil
7. Anwendungsfall
8. Zusammenfassung
Zurück zum Anfang
1. Aufgabenstellung, Zielsetzung
 |
Abb. 1 [1.1]: Entwicklungsphasen für Modelle technischer Probleme (nach Duddeck, 1978) |
Die FE-Methode ist wie alle technischen Verfahren einer Entwicklung unterworfen. Diesen Sachverhalt hat DUDDECK vor einigen Jahren sehr anschaulich dargestellt (Abb.1 [1.1]). Die Jahreszahlen wurden für die FE-Methode ergänzt. Diese entstand in den 50er Jahren, obwohl die Bezeichnung Finite Elemente erst etwas später benutzt wurde. Vorläufer reichen noch viel weiter zurück.
Die Phase II, die komplizierte Phase, war in den 70er und auch noch Anfang der 80er Jahre, als auf Großrechnern gerechnet wurde und die berüchtigten "Waschkörbe" mit Ergebnistabellen erzeugt wurden, in denen dann irgendwo die maßgebenden Ergebnisse standen.
Heute befinden wir uns in der III. Phase, in der der Aufwand auf das notwendige Maß reduziert wird. Der Bericht beschäftigt sich mit der Berechnung von zweidimensionalen Konstruktionen, die als Scheibe gerechnet werden können, wie z.B. Gewichtsstaumauern. Das Ziel ist, die Berechnung zu optimieren, das FE-Netz und die Genauigkeit der Ergebnisse zu verbessern und die Handhabung und den gesamten Berechnungsablauf zu vereinfachen. Das scheint unbedingt notwendig, damit man demnächst auf das Niveau der Linie "1" kommt, bei der der tatsächliche Aufwand dem notwendigen Aufwand entspricht. Dort sind wir noch nicht, wie aus der Praxis bekannt ist. Die FE-Methode ist noch nicht überall akzeptiert; sie gilt als kompliziert und zu aufwendig. Ziel muß sein, optimale FE-Netze zu erzeugen und die Netzerzeugung in geeigneter Weise zu steuern. Für die Steuerung wurde, um es vorweg zu nehmen, die Fuzzylogik verwendet.
Zurück zum Anfang
2. Genauigkeit einer FE-Berechnung
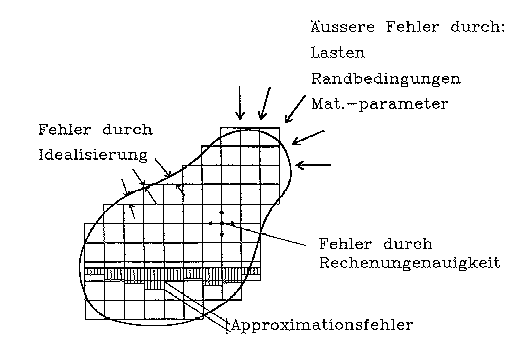 |
Abb. 2 [2.10]: Schematische Unterteilung der Fehlerarten in einer FE-Berechnung |
Zunächst muß etwas zu den Einflüssen auf die Genauigkeit einer FE-Berechnung gesagt werden (Abb.2[2.10]). Vier wesentliche Fehlerarten lassen sich unterscheiden:
- Fehler in den Lasten, den Randbedingungen und den Materialparametern.
Randbedingungen sind die Dirichlet- und Neumann-Randbedingungen, die in einer FE-Berechnung anzusetzen sind. Fehler in den Lasten sind nicht spezifisch für FE-Berechnungen. Es gibt sie genauso bei anderen Berechnungsverfahren. Andere Randbedingungen und die Materialparameter werden zwar für die FE-Berechnung benötigt, nicht aber für manche konventionelle Berechnungsverfahren. Damit ist die Balkentheorie gemeint, mit der die Ergebnisse einer FE-Berechnung im Wasserbau üblicherweise verglichen werden können.
- Fehler durch Idealisierung entstehen bei der Umsetzung des realen Tragwerks oder Berechnungsgebiets in eine Diskretisierung bzw. statisches System. Diese Fehler sind geringer als bei einem konventionellen Berechnungsverfahren, weil die tatsächliche Geometrie viel genauer abgebildet wird.
- Fehler durch Rechenungenauigkeit können bei der Lösung sehr großer Gleichungssysteme auftreten, wenn wiederholt Rechenoperationen zwischen sehr großen und sehr kleinen Zahlen ausgeführt werden. Solche Fehler kann man in den meisten Fällen ausschließen, wenn man in den Computerprogrammen doppelte Zahlengenauigkeit verwendet. Zufällige Fehler in der Computer-Hardware kann man nicht immer ausschließen. Der Ende 1994 bekanntgewordene Fehler im Pentium-Prozessor hätte sich wohl bei FE-Berechnungen bemerkbar gemacht.
- Um die 4. Fehlerart geht es hier: der Approximationsfehler durch die Elemente-Einteilung. Dieser Fehler soll durch eine günstige Einteilung minimiert werden.
Wie kann man nun beurteilen, ob eine Diskretisierung besser ist als eine andere ? Man braucht ein Optimalitätskriterium.
Zurück zum Anfang
3. Fehlerindikator für Elastizitätsprobleme
3.1 Vergleich mit exakter Lösung
Wenn die exakte Lösung eines Problems bekannt wäre, wäre es relativ einfach, den Fehler der FE-Berechnung dieses Problems anzugeben. Man muß nur an jedem Knotenpunkt die Differenz zwischen exakter Lösung und FE-Lösung berechnen und davon das Integral über das gesamte Volumen bilden. Ein daraus gewonnenes Fehlermaß bezeichnet man als Energienorm:
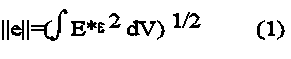
Man kann mathematisch zeigen, daß ein solcher Fehler bei Verfeinerung des FE-Netzes nicht größer werden kann, sondern nur kleiner. Er nimmt in logarithmischer Darstellung geradlinig ab:
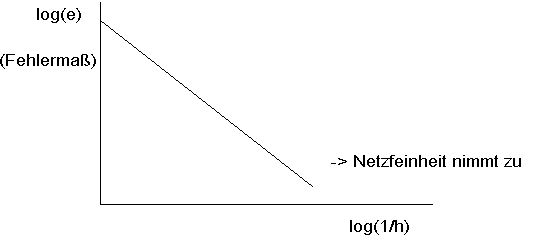 |
Abb. 3: Fehlermaß in Abhängigheit von der Netzfeinheit |
log e = Fehlermaß
log (1/h) = Netzfeinheit
Die exakte Lösung ist in allgemeinen Fällen natürlich nicht bekannt. Deshalb muß man nach einem anderen Weg suchen.
Zurück zum Anfang
3.2 Fehlerindikator aus Spannungssprüngen
Bei der (üblichen) Verschiebungsmethode sind die Knotenverschiebungen die unabhängigen Variablen. Von Element zu Element verlaufen sie stetig entsprechend der Funktion, mit der sie angesetzt wurden. Im Gegensatz dazu sind die Spannungen unstetig. Sie haben an den Elementkanten Sprünge. An einem Knoten gibt es genau so viele unterschiedliche Spannungswerte wie angrenzende Elemente. Die Spannungssprünge sind umso größer, je gröber und unangepaßter die Diskretisierung ist. Es ist daher naheliegend, aus diesen Sprüngen ein Maß für den Fehler abzuleiten. Dafür steht die Formel (2).
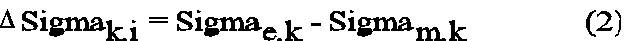
Sigma e,k = Knotenspannung aus einem Element
Sigma m,k = Gemittelte Knotenspannung, mit den Energien der Elemente gewichtet
Zweckmäßigerweise geht man dann zu Differenzenergien über. Dazu führt man folgende Matrizenmultiplikation aus:

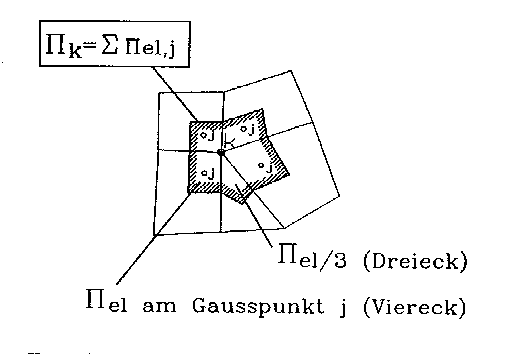 |
Abb. 4 [2.7]: Teilenergien am Knoten k |
Diese Differenzenergien müssen jetzt noch geeignet gewichtet und gemittelt werden. Als Wichtungsfaktor werden wieder die Elementenergien gewählt (Abb.4 [2.7]):
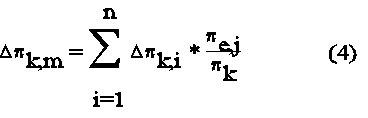
Damit hat man für jeden Knotenpunkt einen Wert für die Differenzenergie an diesem Punkt. Er muß nun auf einen geeigneten Wert bezogen werden, damit man einen prozentualen Energiefehler erhält. Als Bezugswert wird ein Teil der Gesamtenergie gewählt, nämlich der Teil, der auf den Knoten entfallen würde, wenn die Gesamtenergie gleichmäßig verteilt wäre:
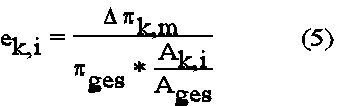
Dies ist der gesuchte Fehlerindikator je Knotenpunkt. Der Gesamtfehler der Diskretisierung ist die Summe dieser Einzelfehler. Er ist die Summe der Beträge der einzelnen Knotenfehler, bezogen auf die Gesamtenergie:
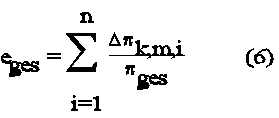
Diesen Gesamtfehler oder Fehlerestimator kann man auch als "Restfehler" bezeichnen, weil er angibt, wieviel restliche Ungenauigkeit noch in der Diskretisierung steckt.
Zurück zum Anfang
4. Aufbau von FE-Netzen
Mit dem gefundenen Fehlerindikator und Restfehler werden jetzt FE-Netze beurteilt. Das geschieht auf 3 Stufen (Abb.5 [3.1.1]):
* nämlich auf der Stufe der Elemente mit ihren Eigenschaften,
* bei der Netzform mit seinen Eigenschaften,
* und beim Berechnungsraum (siehe unten).
 |
Abb. 5 [3.1.1]: Schematische Ebenen beim Vorgang einer Diskretisierung |
Zurück zum Anfang
4.1 Elementeigenschaften
4.1.1 Elementart
Die ersten beiden Punkte lassen sich an einem einfachen Kragarm behandeln, der schon häufig in der Literatur untersucht wurde, z.B. von Zienkiewicz [1]. Für den Kragarm gibt es auch eine analytische Lösung. Er hat die Abmessungen 3*1m, ist an einer Seite eingespannt und an der anderen mit einer Vertikallast von "V=1" belastet.
Zienkiewicz hat damals verschiedene Elementarten untersucht, hat aber nur drei Elemente benutzt bzw. die kleinstmögliche Anzahl.
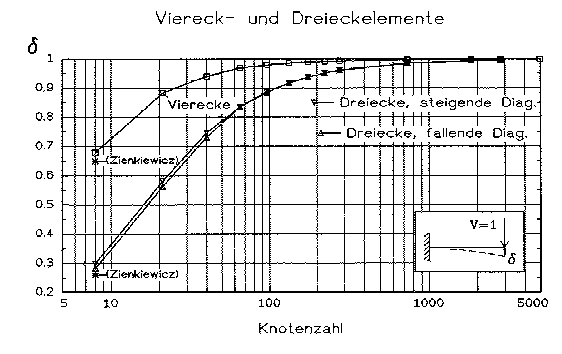 |
Abb. 6 [3.1.12]: Dimensionslose Absenkung delta bei x=L bei wachsenden Knotenzahlen infolge einer vertikalen Last (V=1) am Ende des Kragarms (Balkentheorie=1) |
Unter dem Stichwort "Elementart" wird nun der Unterschied zwischen Dreiecken und Vierecken herausgegriffen. Beide liefern unterschiedliche Ergebnisse bei der statischen Berechnung in diesem Kragarm (Abb.6 [3.1.12]). In dieser Abbildung sieht man die Absenkung des Kragarmendes bei steigender Knotenzahl für Dreieck- und Viereck-Diskretisierungen. Man sieht, daß unter Verwendung sehr vieler Knoten das genaue Ergebnis in beiden Fällen erreicht wird. Die Vierecke konvergieren aber sehr viel schneller: schon bei 200 Knoten ist das Vergleichsergebnis nach der Balkentheorie bzw. Elastizitätstheorie erreicht, bei Dreiecken erst bei 1000 Knoten. Dabei macht es in diesem Fall fast keinen Unterschied, ob die Dreiecke steigende oder fallende Diagonalen haben. - Zienkiewicz´s Ergebnisse sind als Sternchen eingetragen. Sie weichen geringfügig von den hier berechneten Ergebnissen ab, weil nicht alle Randbedingungen zu klären waren, mit denen er gerechnet hat.
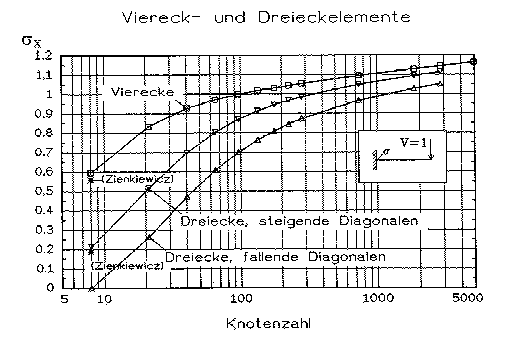 |
Abb. 7 [3.1.13]: Dimensionslose Spannung Sigma x bei x=L bei wachsenden Knotenzahlen infolge einer vertikalen Last (V=1) am Ende des Kragarms (Balkentheorie=1) |
In der nächsten Abbildung (7 [3.1.13]) sind für denselben Lastfall die Spannungen an der Einspannstelle dargestellt. Man sieht sofort den Unterschied zur vorigen Abbildung: die Spannungen konvergieren nicht. Sie wachsen über den Referenzwert nach der Balkentheorie hinaus. Die Vierecke liegen dabei immer über den Dreiecken. Bei den Dreiecken spielt es eine große Rolle, ob sie steigende oder fallende Diagonalen haben. Die Ergebnisse weichen ungefähr so stark voneinander ab wie Dreiecke und Vierecke voneinander abweichen.
Der Unterschied zwischen den Dreiecksformen hängt im wesentlichen davon ab, wie das Dreieck an der Einspannstelle aussieht. Da in den Dreiecken die Spannung konstant ist, ist es sehr wichtig, wie nahe sein Schwerpunkt an dieser Stelle liegt. Links oben kommt ein Dreieck mit steigender Diagonale der Ecke am nächsten, links unten ist es umgekehrt.
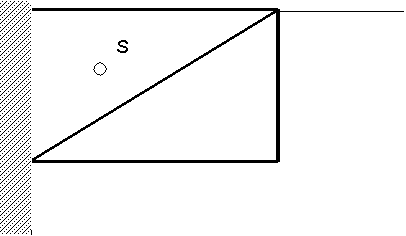 |
Abb. 8: Dreieckschwerpunkt in der Nähe der Einspannstelle |
Einen exakter Zahlenwert für die Spannung an der Einspannstelle ist nicht faßbar- es gibt ihn gar nicht, denn er hängt von der Größe der Elemente ab.
 |
Abb. 9 [3.1.14]: Dimensionslose Innere Energie (Balkentheorie=1) und Restfehler bei wachsenden Knotenzahlen infolge einer vertikalen Last (V=1) am Ende des Kragarms |
Wie genau sind nun diese Elemente ? In dieser Abbildung (9 [3.1.14]) sieht man, daß der Restfehler bei wachsender Knotenzahl gegen Null konvergiert, und zwar bei Vierecken wesentlich schneller als bei Dreiecken.
Außerdem ist noch die innere Energie dargestellt, die gegen den Endwert der analytischen Lösung konvergiert. Dieser Wert läßt sich aus dem Produkt von Spannungen und Verformungen berechnen. Auch hier konvergieren Vierecke schneller.
Aus den gezeigten Abbildungen kann man folgern, daß Vierecke in elastostatischen Berechnungen besser geeignet sind als Dreiecke. Nur da, wo die Geometrie des Berechnungsgebietes es erfordert, sollte und darf man Dreiecke verwenden.
Nach der Elementart wird der Einfluß der Elementgestalt auf die Berechnung dieses Kragarms vorgestellt. Darunter fallen:
* das Seitenverhältnis der Elementkanten
* und die Verzerrung der Elemente, ausgedrückt durch die Winkel der Kanten.
Bei beiden werden nur die wesentlichsten Ergebnisse gezeigt.
Zurück zum Anfang
4.1.2 Seitenverhältnis
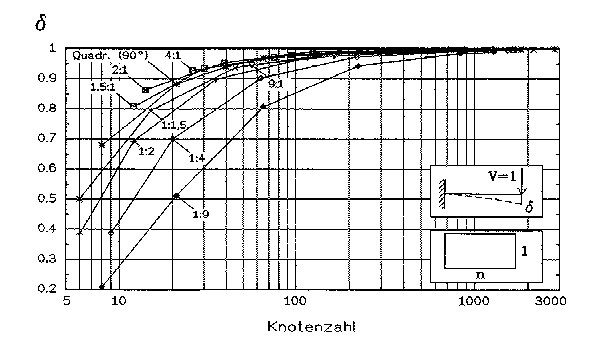 |
Abb. 10 [3.1.19]: Dimensionslose Absenkung delta am Ende des Kragarms infolge einer vertikalen Last (V=1) in Abhängigkeit vom Seitenverhältnis 1:n der Vierecke (Balkentheorie=1) |
Das Seitenverhältnis ist definiert mit 1:n. 1:2 steht z.B. für ein liegendes Element, das doppelt so breit wie hoch ist (Abb.10 [3.1.19]). Man sieht, daß Elemente mit ungünstigem Seitenverhältnis schlechte Ergebnisse liefern. Dabei macht es aber einen Unterschied, ob die Elemente längs oder quer zur Belastungsrichtung liegen.
Das gleiche gilt auch für die Spannung an der Einspannstelle.
Hochkant stehende Elemente (2:1, 4:1) liefern bei kleinen Knotenzahlen ein geringfügig besseres Ergebnis für die Verformung als quadratisch geformte. Liegende Elemente dagegen führen zu einem ungünstigeren Ergebnis.
Während hochkant stehende Elemente fast den gleichen Spannungswert liefern wie quadratische Elemente, bringen liegende Elemente einen zu niedrigen Wert für die Spannung.
Man kann bei einem Tragwerk die Elemente nicht immer entsprechend der Belastungsrichtung ausrichten; deshalb empfiehlt es sich, allgemein nur Elemente bis zum Seitenverhältnis 1:2 bzw. 2:1 zuzulassen und längere ggf. in der langen Richtung zu unterteilen.
Zurück zum Anfang
4.1.3 Elementform
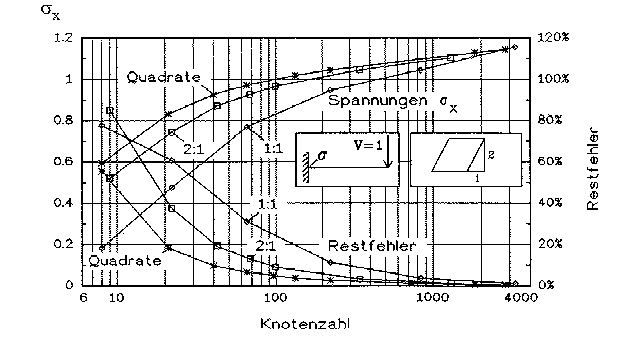 |
Abb. 11 [3.1.23]: Dimensionslose Spannung Sigma x (Balkentheorie=1) und Restfehler in Abhängigkeit von der Form der Elemente |
Mit der Form der Elemente ist die Neigung der Kanten gemeint. Sie gibt also an, wie stark die Elemente verzerrt sind (Abb.11 [3.1.23]).
Je flacher der Neigungswinkel der Parallelogrammkanten ist, desto verzerrter ist das Element. Bei den drei oberen Kurven in der Abb. nimmt die Verzerrung von oben nach unten zu.
Die oberste Kurve ist die Referenzkurve für quadratische Elementformen, bei der untersten sind die Kanten um 45° geneigt.
Dargestellt ist die Spannung *x an der Einspannstelle. Das Ergebnis ist: bei kleinen Knotenzahlen sind verzerrte Elemente deutlich ungünstiger als unverzerrte; bei großen Knotenzahlen nimmt der Unterschied wieder ab. -
Im unteren Teil der Abbildung sieht man den Restfehler, der zu den Spannungen sozusagen komplementär verläuft. Bei kleinen und mittleren Knotenzahlen ist der Fehler doppelt bzw. 4 mal so groß, wenn die Kanten verzerrt sind. Erst bei 2000 und mehr Knoten macht die Verzerrung kaum noch etwas aus.
Wenn man also genügend Knoten und Elemente verwendet, kann man Verzerrungen in Kauf nehmen.
Zurück zum Anfang
4.2 Netzformen
Die zweite Stufe beim Aufbau eines FE-Netzes ist die Netzform. Die Abb. 12 zeigt einige regel- und unregelmäßige Netze, die für die nachfolgenden Berechnungen verwendet wurden.
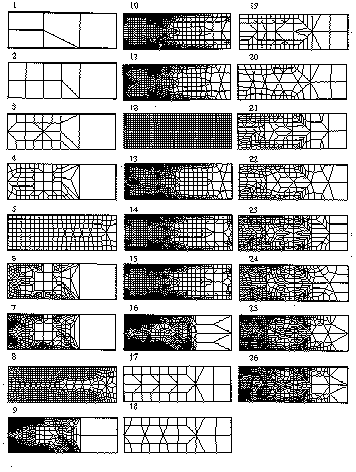 |
Abb. 12 [3.2.5]: Netzformen |
Zurück zum Anfang
4.2.1 Unregelmäßigkeit
FE-Netze können unregelmäßig und unsymmetrisch sein und ungleich große Elemente haben. Die Netzform kann mit einem empirischen Faktor "Un" für "Unregelmäßigkeit“ klassifiziert werden. In diesen gehen ein:
1. ein Formfaktor 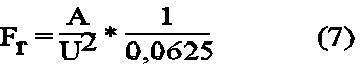
0,0625 ist dabei der ideale Formfaktor eines Quadrats.
2. ein Determinantenfaktor für den Winkel zwischen den Elementkanten: 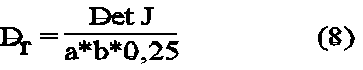
0,25 ist der ideale Determinantenfaktor einer 90°-Ecke.
3. und ein Kantenfaktor, der die Parallelität zur X- oder Y-Achse angibt: 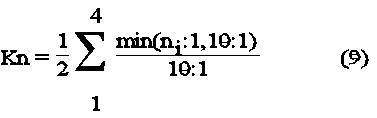
Un=1 ist die größte Ordnung,
Un=0 ist die größte Unordnung.
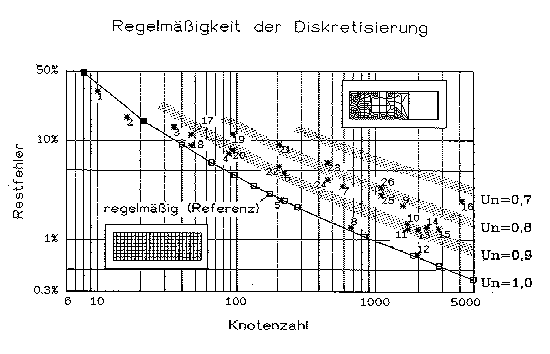 |
Abb. 13 [3.2.3]: Restfehler in Abhängigkeit von der (Un-)Regelmäßigkeit ("Un") des FE-Netzes |
Die Restfehler verschiedener regel- und unregelmäßiger Diskretisierungen sind in der Abbildung (13 [3.2.3]) eingetragen. Für die Unregelmäßigkeit lassen sich nun mit einer gewissen Bandbreite Höhenlinien (oder Höhenbänder) angeben, so daß man, wenn man die Anzahl der Knoten und die Unregelmäßigkeit kennt, schon vor der Berechnung sagen kann, wie groß der Restfehler sein wird. Mit dieser Hilfe kann man schon von Anfang an von einem Startnetz ausgehen, das einen niedrigen Fehler erwarten läßt.
Zurück zum Anfang
4.2.2 Unsymmetrie und Größenverhältnis
Zwei spezielle Formen der Unregelmäßigkeit sind Unsymmetrie und Größenverhältnis der Elemente. Beide führen ebenfalls zu ungenaueren Ergebnissen.
Von zwei weiteren Untersuchungen wird nur je eine charakteristische Abbildung gezeigt:
1. der Einfluß einer unsymmetrischen Diskretisierung (Abb.14 [3.2.8]) und
2. der Einfluß des Größenverhältnisses der Elemente (Abb.15 [3.2.14]).
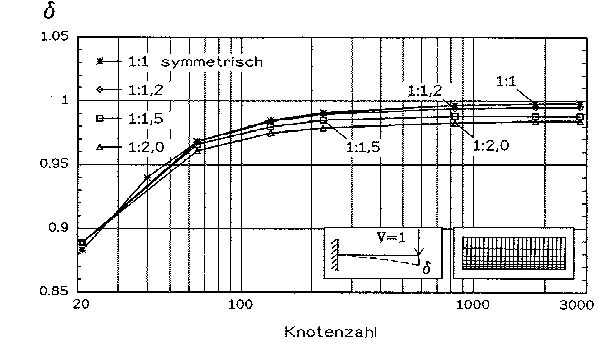 |
Abb. 14 [3.2.8]: Dimensionslose Absenkung delta am Ende des Kragarms in Abhängigkeit von der Unsymmetrie des Netzes (Balkentheorie=1) |
Hier ist der Kragarm mit Elementen diskretisiert worden, deren Größe von oben nach unten abnimmt, mit einem variablen Verhältnis der Elementgrößen untereinander. Je größer dieses Verhältnis ist, desto ungenauer wird die berechnete Absenkung des Kragarmes. Der richtige Grenzwert wird auch bei nur geringer Unsymmetrie nicht ganz erreicht, aber immerhin noch zu 98% in der untersten Kurve.
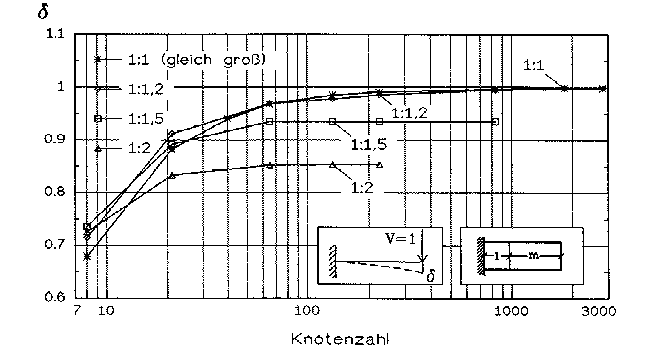 |
Abb. 15 [3.2.14]: Dimensionslose Absenkung delta am Ende des Kragarms infolge einer vertikalen Last (V=1) in Abhängigkeit vom Größenverhältnis 1:m der Elemente (Balkentheorie=1) |
Weniger genau aber ist eine Diskretisierung, bei der in beiden Richtungen die Elementgrößen unterschiedlich sind. Dafür ist die Diskretisierung hier symmetrisch zur Mittelachse. Bereits bei einem Größenverhältnis von 1:2 wird die Absenkung nur zu 85% erfaßt. Der Restfehler verhält sich ähnlich ungünstig. - Solch ein Größenverhältnis zwischen benachbarten Elementen (nämlich 1:2) kommt in der Praxis aber noch häufig vor.
Aus dem Gesagten folgt, daß eine möglichst regelmäßige Netzform die beste wäre. Gleichzeitig braucht man möglichst viele Elemente. Beides auf einmal ist nicht möglich, da zu viele Elemente notwendig wären. Also muß man als Kompromiß optimale Netze erzeugen.
Zurück zum Anfang
5. Generierung optimaler FE-Netze
Dazu können zwei Verfahren dienen:
1. die Netzglättung und
2. die Netzverfeinerung.
5.1 Netzglättung
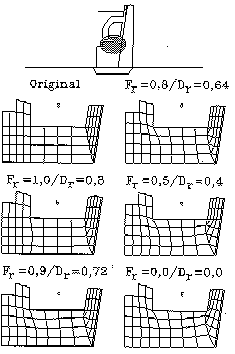 |
Abb. 16 [4.1.3]: Netzveränderung durch Glättung mit verschiedenen Form- und Determinantenfaktoren |
In Abb.16 [4.1.3] ist ein Beispiel für eine Netzglättung zu sehen. Die Knotenpunkte eines FE-Netzes werden dabei verschoben. Jeder Knoten erhält die gemittelten Koordinaten aller benachbarten Knoten. Diese Knotenverschiebung kann man aber nicht frei laufen lassen, denn es würden auch unmögliche Elementformen entstehen, z.B. bekäme das Dreieck an der inneren rechten Ecke die Fläche Null. Also muß man Formkontrollen einbauen, wofür sich der „Formfaktor Fr“ und der „Determinantenfaktor Dr“ eignen. Man sollte die Netzglättung etwa bis links unten zulassen, weil dann die Berechnung genauer wird, wie in der nächsten Abbildung zu sehen ist (17 [4.1.7]).
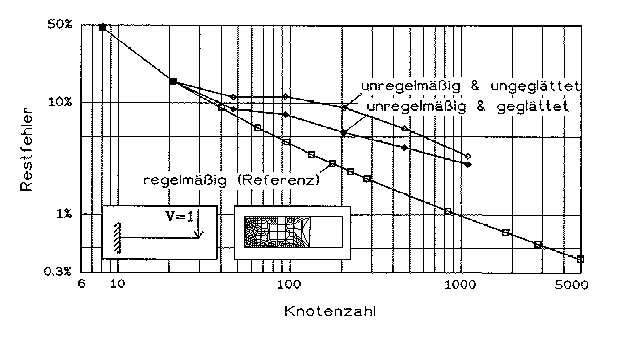 |
Abb. 17 [4.1.7]: Restfehler im Kragarm mit und ohne Netzglättung |
Hier wird für einige unregelmäßige Diskretisierungen des bereits bekannten Kragarmes gezeigt, daß eine Netzglättung den Restfehler vermindert.
Die unterste Kurve ist die Referenzkurve mit quadratischen Elementformen. Die obere Kurve gilt für unregelmäßige, ungeglättete FE-Netze. In der mittleren Kurve sind diese Netze geglättet. Hier z.B. geht der Fehler z.B. von etwa 10% auf etwa 5% zurück.
Zurück zum Anfang
5.2 Adaptive Netzverfeinerung
Das zweite Verfahren ist die Netzverfeinerung. Adaptiv heißt anpassend, d.h. daß das FE-Netz an das Problem angepaßt wird und daß man an die genaue Lösung immer näher herankommt.
5.2.1 h- und p-Version
Man unterscheidet die h-Version und die p-Version der Verfeinerung. In der h-Version werden die Elemente in kleinere Elemente aufgeteilt, und in der p-Version wird der Grad der Ansatzfunktion erhöht. Hier wird nur die h-Version verwendet, weil man damit beliebig viele Schritte ausführen kann - nicht nur so viele, wie bei der p-Version im Programm vorgesehen sind. Außerdem ist die p-Version nicht für nichtlineare Berechnungen geeignet.
Zurück zum Anfang
5.2.2 Steuerungsparameter
Eine Verfeinerung eine FE-Netzes muß gesteuert werden. Es gibt dafür viele Gesichtspunkte, z.B.:
1. Erfahrung und Gefühl (z.B. bei großen Spannungsunterschieden sind kleine Elemente nötig)
2. geometrische Bedingungen (Krümmungsradien nachbilden)
3. ein Fehlerindikator bzw. Verfeinerungsindikator.
Ein Fehlerindikator ist dabei besonders wichtig, weil er objektiv ist und weil man dann automatisch verfeinern kann. Er muß aber von anderen Kriterien ergänzt werden, z.B.: Elementform, Grenzlänge von Kanten, Richtung der Kanten usw.
Alle diese Kriterien sind verschieden wichtig, sie können sich gegenseitig unterstützen oder auch widersprechen bei der Entscheidung, ob eine Elementkante geteilt werden soll oder nicht. In solchen Fällen bietet sich die Fuzzylogik an. Das Wort kommt von dem englischen "fuzzy", das soviel wie "unscharf, fusselig" bedeutet.
Diese Technik wird, besonders in Japan, dazu benutzt, Anlagen und Geräte zu steuern. Sie ist immer dann vorteilhaft, wenn ein erfahrener menschlicher Experte nach Gefühl entscheiden würde. Für FE-Netze ist diese Methode eine Neuerung.
Zurück zum Anfang
5.2.3 Fuzzysteuerung
Ein Beispiel: Für einen Menschen soll entschieden werden, ob er jung oder alt ist. Nach konventioneller Logik müßte man eine Grenze festlegen, z.B. 45 Jahre. Darunter ist ein Mensch jung, darüber ist er alt. Das hieße, mit 44 ist man jung, mit 46 alt. Das ist unbefriedigend. Nach der Fuzzylogik würde man es folgendermaßen entscheiden (Abb.18):
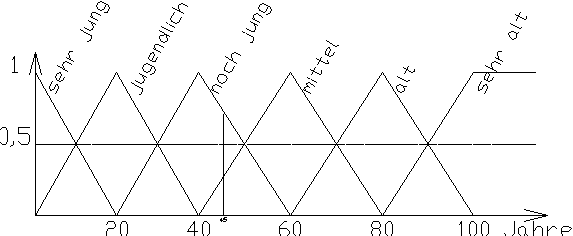 |
Abb. 18: Fuzzyfunktion für das Alter eines Menschen |
Dies ist eine Fuzzyfunktion. Jedes Dreieck deckt einen Bereich des Alters ab. Ein Mensch mit 45 Jahren hätte so die Eigenschaften:
1. noch jung mit der Wertung 0,75 und
2. mittleres Alter mit der Wertung 0,25.
Man stellt solche Fuzzyfunktionen auf, indem man „Experten“ befragt.
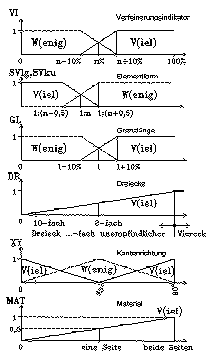 |
Abb. 19 [4.3.6]: Fuzzy-Funktionen für eine Netzverfeinerung |
Die weiteren Schritte der Fuzzy-Methode werden direkt an der Verfeinerung von FE-Netzen erläutert (Abb.19 [4.3.6]). Dies sind die Fuzzyfunktionen für die Kriterien, nach denen eine Elementkante unterteilt wird. Das erste ist der Verfeinerungsindikator. Der Anteil n muß gewählt werden. Kanten, deren Indikatorwert weit über n liegen, bekommen die Eigenschaft "Viel" mit der Wertung 1, solche, die weit darunter liegen, diese Eigenschaft mit der Wertung 0. Außerdem gibt es Zwischenwerte von 0 bis 1.
Die anderen Fuzzyfunktionen bedeuten folgendes:
1. Die zweite Funktion bewirkt, daß lange Kanten unterteilt werden, und daß günstige Seitenverhältnisse entstehen.
2. Die dritte Funktion gilt für eine Grenzlänge für eine Kante, die nicht unterschritten werden soll.
3. Die vierte Funktion bewirkt, daß Dreiecke weniger leicht geteilt werden als Vierecke. Das ist sinnvoll, um regelmäßige Netze zu erzeugen.
Außerdem gibt es noch Funktionen für die Kantenrichtung und für den Materialtyp.
1. Die fünfte Funktion erteilt allen Kanten eine Wertung dafür, horizontal oder vertikal zu sein.
2. Die sechste Funktion gibt an, ob sie auf einer oder beiden Seiten in einem Materialbereich liegt, der beliebig verfeinert werden darf und nicht in einem Bereich, der möglichst ausgeschlossen werden soll.
Jetzt werden noch die folgenden Definitionen benötigt:
Es gibt 6 Dringlichkeitsstufen für die Unterteilung von "sehr sehr viel" bis "sehr sehr wenig". Für jede Stufe wird eine Aussage gebraucht.
| WWW
| sehr sehr wenig
|
| WW
| sehr wenig
|
| W
| wenig
|
| V
| viel
|
| VV
| sehr viel
|
| VVV
| sehr sehr viel
|
Tab.1: Dringlichkeitsstufen für die Unterteilung
Eine Aussage ist ein Wert zwischen 0 und 1, und man erhält ihn aus den Fuzzyregeln. Die Fuzzyregeln können mit UND, ODER oder NICHT verknüpft werden, die in dieser Tabelle stehen.
Von den Regeln kann es beliebig viele geben. Sie können ein, zwei oder mehr Kriterien enthalten, gerade so, wie es nötig ist, um das Problem hinreichend zu beschreiben. Eine Regel lautet z.B.:
Wenn Verfeinerungsindikator = viel und
Seitenverhältnis = ungünstig und
Kante ist horizontal oder vertikal dann
Unterteilung = ist sehr sehr viel
Wichtig ist, daß man genug Regeln hat, um für jede Dringlichkeitsstufe ein Ergebnis zu bekommen. - Bekommt man für eine Stufe mehrere Werte, nimmt man den größten.
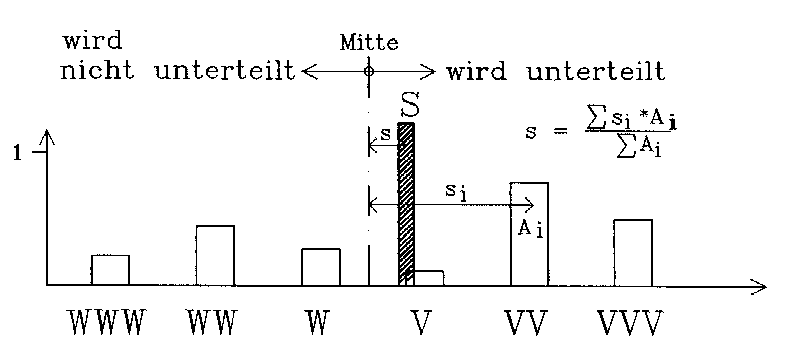 |
Abb. 21 [4.3.10]: Auswertung der Fuzzywerte für die Unterteilung einer Kante |
Die Werte für alle Stufen werden nun für jede Elementkante als Balken aufgetragen (Abb.21 [4.3.10]). Entscheidend ist nun, wo der Schwerpunkt liegt. Liegt der Schwerpunkt rechts von der Mitte, wird die Kante unterteilt, sonst nicht. Bei anderen Problemen könnte man hieraus z.B. die Stellung eines Ventils ablesen, die einen Wert zwischen 0 und einem Maximum hat.
Nachdem man das Verfahren für alle Elementkanten durchgeführt hat, hat man einen Verfeinerungsschritt gemacht. Mit dem neuen FE-Netz macht man eine neue Berechnung, verfeinert dann noch mal usw.
Es gibt nun verschiedene Verfeinerungsstrategien, bei denen in mehreren Schritten verschieden stark verfeinert wird. Das wird an einem Fallbeispiel gezeigt.
Zurück zum Anfang
6. Fallbeispiel: Staumauer mit Dreieckprofil
Das Fallbeispiel ist eine sehr einfachen Staumauer mit einem Dreiecksprofil.
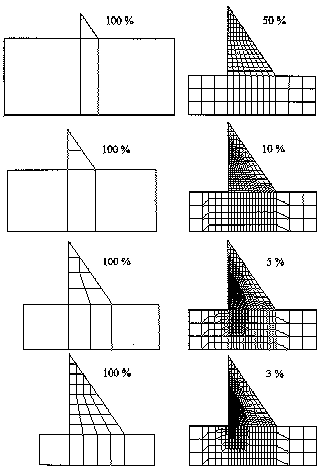 |
Abb. 22 [5.4.1]: FE-Netze in 8 Verfeinerungsschritten für ein Fallbeispiel |
Zu sehen ist in Abb.22 [5.4.1] das FE-Netz in mehreren Schritten. Links oben ist das erste FE-Netz. Es besteht aus 4 „Master“-Elementen. In den ersten Schritten werden fast alle Elemente unterteilt. Nebenbedingungen sorgen dafür, daß z.B. das mittlere schmale Element nur horizontal geteilt wird. Später werden nicht mehr alle Elemente unterteilt, wie an den Prozentsätzen zu sehen ist. Übergangsbereiche werden nicht weiter unterteilt.
Das Netz konzentriert sich dort, wo es auch aus Erfahrung notwendig ist: am wasserseitigen Mauerfuß.
In der nächsten Abbildung (22a [5.2.5]) ist der Restfehler bei dieser Strategie dargestellt. Wie man an der untersten Kurve sehen kann, sinkt er von 22% auf 2%.
Die Netzunregelmäßigkeit wird vom 1. bis zum letzten Netz nur wenig größer; sie liegt bei 0,97.
 |
Abb. 23 [5.4.8]: Dimensionslose Spannungen Sigma y am wasserseitigen Mauerfuß in Abh. von der Elementgröße (Scheibentheorie=1) |
Der wasserseitige Fußpunkt ist ein Problem. Für die Genauigkeit der Berechnung müßte er immer feinere Elemente unterteilt werden. Weil die einspringende Ecke aber eine Singularität ist, führt das zu unendlich großen Spannungen. Dies zeigt die nächste Abbildung (23 [5.4.8]). Auf der x-Achse ist der Kehrwert der Elementgröße angegeben. Die Elemente werden nach rechts immer kleiner. Auf der y-Achse ist die Spannung *y aufgetragen, beides logarithmisch. Man sieht, daß in beiden Lastfällen (Eigengewicht und Wasserdruck) und auch deren Summe sich Geraden ergeben. Das heißt, die Spannungen streben ins Unendliche. Es hat daher keinen Sinn, die Netzverfeinerung hier immer weiter zu treiben, sondern man muß bei einer gewissen Elementgröße aufhören.
An diesem Fallbeispiel läßt sich nun auch das zeigen, was bei dem Kragarm (s.o.) weglassen werden mußte: der Einfluß des Berechnungsraumes. Wie groß muß er sein, d.h. wie tief muß der Untergrund sein, damit die Ergebnisse für die Staumauer gegen die richtige Lösung konvergieren ? Das soll an der Verformung der Mauerkrone gezeigt werden.
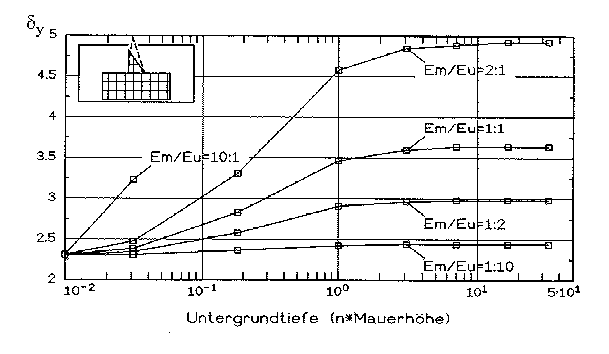 |
Abb. 24 [5.3.5]:Dimensionslose Vertikalverschiebung delta y der Mauerkrone im Lastfall Wasserdruck in Abh. von Untergrundtiefe und E-Modul-Verhältnis Em/Eu (Scheibentheorie=1) |
In dieser Abbildung (24 [5.3.5]) ist die Verschiebung dy der Mauerkrone aufgetragen, in Abhängigkeit von der Tiefe des Untergrundes. Die verschiedenen Kurven gelten für verschiedene E-Modul-Verhältnisse zwischen Mauer und Untergrund. In allen Fällen konvergiert die Vertikalverschiebung dy gegen einen Grenzwert, wenn der berücksichtigte Untergrund tiefer wird. Bei ca. 3-facher Mauerhöhe ist der Grenzwert fast erreicht, bei 10-facher Mauerhöhe ganz erreicht. Das heißt, der Berechnungsausschnitt sollte mindestens die dreifache Höhe der Mauer haben und dann auch genauso weit nach beiden Seiten reichen.
Zurück zum Anfang
7. Anwendungsfall
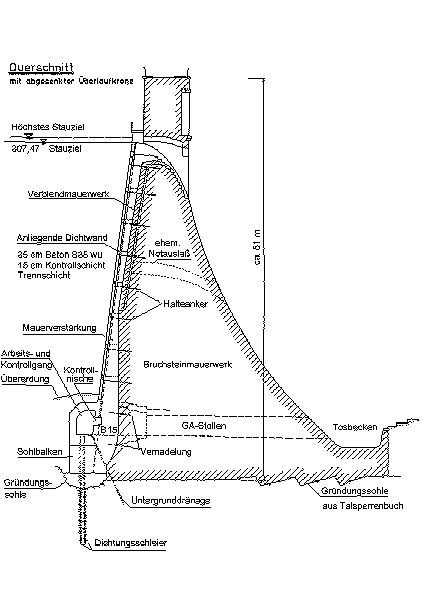 |
Abb. 25 [A.1]: Regelquerschnitt des Anwendungsfalles |
Die Abbildung zeigt einen praktischen Anwendungsfall (Abb.25 [A1]). Es ist eine Gewichtsstaumauer mit einer Verstärkung und einer vorgesetzten Dichtwand. Man sieht die verschiedenen Materialbereiche, die bei der ersten Einteilung beachtet werden müssen. Sie sind teilweise so geformt, daß es ziemlich schwierig ist, ein günstiges erstes Startnetz zu finden.
 |
Abb. 26 [A.5]: Rand und Materialbereiche mit Innenknoten (Ausschnitt) |
In diesem Bild sieht man die ersten Knoten: an den Rändern, an den Materialgrenzen und auch bereits einige Knoten im Innern, die notwendig sind, um die ersten Elemente zu erzeugen (Abb.26 [A5]).
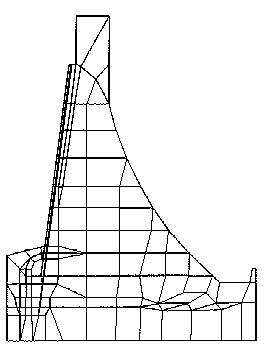 |
Abb. 27 [A.7]: Ausgangs-FE-Netz (Ausschitt) |
 |
Abb. 28 [A.12]: FE-Netz nach dem 1. Verfeinerungsschritt |
 |
Abb. 29 [A.14]: FE-Netz nach dem 2. Verfeinerungsschritt |
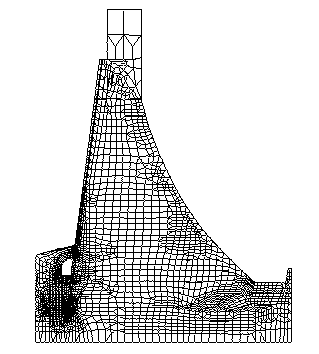 |
Abb. 30 [A.16]: FE-Netz nach dem 3. Verfeinerungsschritt |
In den letzten Bildern sind die FE-Netze dieses Beispiels in vier Schritten zu sehen (Abb.27-30 [A7, A12, A14, A16]). Das Netz wird dort immer feiner, wo aus Erfahrung die kritischen Bereiche sind: an den Rändern, wo die stärkste Belastung ist, am luftseitigen Mauerfuß, am wasserseitigen Mauerfuß, am Kontrollgang usw.
Zurück zum Anfang
8. Zusammenfassung
In dem Bericht wurden gezeigt:
1. ein Fehlerindikator als Optimalitätskriterium zur Beurteilung von FE-Netzen,
2. die Einflüsse auf die Genauigkeit einer Berechnung,
3. ein Unregelmäßigkeitsfaktor, mit dem die Genauigkeit einer Diskretisierung im voraus abgeschätzt werden kann,
4. eine Verfeinerungsstrategie, mit der ein optimales FE-Netz erzeugt werden kann,
5. und die Steuerung der Verfeinerung mit der Fuzzy-Technik.
Mit diesem Algorithmus wird die Genauigkeit einer FE-Berechnung gesteigert, außerdem wird die Berechnung einfacher gemacht und verkürzt. Als Anwendungsbeispiel dient die Generierung des FE-Netzes für eine Gewichtsstaumauer.
Literatur:
Duddeck: Statische Berechnungen im Fels- und Tunnelbau, in: Pahl, Stein, Wunderlich (Hrsg.): Finite Elemente in der Baupraxis, 1978
Hoffmann, M.: Automatische Generierung von FE-Netzen für Scheibenkonstruktionen am Beispiel von Gewichtsstaumauern, Mitteilungen des Instituts für Wasserwirtschaft, Heft 99, Aachen 1995
Zienkiewicz, O. C.: Methode der finiten Elemente, München 1984
Zurück zur Homepage
Seite erstellt am 26.1.1997 von M. Hoffmann. Zuletzt aktualisiert am 2.8.1997. Zurück zum Anfang